function [matLEA,neg_log_corr_sp] = knnlea(matCoordinates,matFeature,K,matContinuousVar)
% Local enrichment analysis (LEA) using K Nearest Neighbors
%   written by Yannik Severin & Berend Snijder, 2021. email
%   bsnijder@gmail.com for more information.
%
% Usage:
%   [matLEA,neg_log_corr_sp] = knnlea(matCoordinates,matFeature,K,matContinuousVar)
%
% LEA probes the local neighborhood around each single sample (rows) in a
% defined multidimensional space (columns) and calculates the probability
% to randomly find n-sample of condition X (definded by matFeature) using a
% hypergeometric distribution function (taking into account the total
% number of drawn cells, the total number of cells in the whole space and
% the total number of cells of condition X in the space). A neighborhood
% around an single sample is defined as the K-nearest neighbours around the
% probed sample. The calculated enrichment-probability for condition X gets
% assigned to original sample of the probed region and the approach is
% iterated for each single sample in the given space.
%
% matCoordinates = spatial x and y positions of each single sample.
% matFeature = categorical classes of each single sample
% K = number of nearest neighbours to define the local neighbourhood,
%   defaults to K = 200.
% matContinuousVar = optional, if given leah calculates if a second
%   variable is correlated in the probed neighborhood.
%
% outputs:
%
% matLEA = the signed neg-log10-transformed enrichment or depletion P-value
%   as calculated by a hypergeometric test.
% neg_log_corr_sp = the neg-log10-transformed P value of the local spearman
%   correlation coefficient.
%
% Example usage:
%   knnlea()
%
%   Running knnlea() without inputs will produce a test result on standard
%   matlab data using:
%       objTmpData = load('fisheriris.mat');
%       matCoordinates = objTmpData.meas;
%       matFeature = strcmpi(objTmpData.species,'versicolor');
%       K = 10;

    if nargin<3
        K = 200;
    end

    if nargin==0
        % in demo mode, we run on the standard "fisheriris" matlab dataset
        fprintf('%s: Running in DEMO mode\n',mfilename)
        objTmpData = load('fisheriris.mat');
        matCoordinates = objTmpData.meas;
        matFeature = strcmpi(objTmpData.species,'versicolor');
        K = 10;
    end

    % init output and start calculation
    matLEA = NaN(size(matFeature));
    if nargout>1
        neg_log_corr_sp = NaN(size(matFeature));
    end

    % look up the nearest neighbor for each cell
    idx = knnsearch(matCoordinates,matCoordinates,'K',K);

    % if matFeature is logical/discrete, then calculate the hypergeometric
    % LEA scores
    if isequal(matFeature(~isnan(matFeature)), logical(matFeature(~isnan(matFeature))))
        fprintf('%s: Calculating local hypergeometric LEA scores\n',mfilename)

        for i = 1:size(matFeature,2)

            matF = matFeature(:,i);

            matKNNFeature = matF(idx);

            % calculate hypergeometric enrichment
            matLEA_P_U = hygecdf(nansum(matKNNFeature,2),sum(~isnan(matF)),nansum(matF(:)),sum(~isnan(matKNNFeature),2),'upper');
            % calculate hypergeometric depletion
            matLEA_P_D = hygecdf(nansum(matKNNFeature,2),sum(~isnan(matF)),nansum(matF(:)),sum(~isnan(matKNNFeature),2));

            matLEA_P_U = fixinfs(-log10(matLEA_P_U));

            matLEA_P_D = fixinfs(-log10(matLEA_P_D));

            matLEA(:,i) = matLEA_P_U;

            matLEA(matLEA_P_U<matLEA_P_D,i) = -matLEA_P_D(matLEA_P_U<matLEA_P_D);

            % if the cell itself had a NaN-feature value, set the KNN-mean to
            % NaN as well...

            matLEA(isnan(matKNNFeature(:,1)),i) = NaN;
        end

    else

        warning('bs:Bla','%s: Not calculating the hypergeometric LEA scores as the second input (matFeature) is not discrete',mfilename)

    end

    % calculate correlations if a continuous variable is passed.
    if nargin==4

        neg_log_corr_sp = nan(size(matFeature,1),size(matContinuousVar,2));

        fprintf('%s: Calculating local spearman correlations\n',mfilename)

        gIND = vec2ind(matFeature')';

        gIND = gIND(idx);

        matCountPerClass = sum(matFeature);

        [x] = cell2mat(cellfun(@(c) countUnique(c,1:size(matFeature,2)), num2cell(gIND, 2),'uni',0));

        x_rel = x./repmat(matCountPerClass,[size(matFeature,1),1]);

        for i = 1:size(matContinuousVar,2)

            if all(~isnan(x_rel(:))) && all(~isnan(matContinuousVar(:,i)))
                % if there's no NaNs, this is much faster
                [corr_sp,pCorr] = corr(x_rel',matContinuousVar(:,i),'type','spearman');
            else
                % if there are NaNs, we have to go slow with 'rows','pairwise
                [corr_sp,pCorr] = corr(x_rel',matContinuousVar(:,i),'rows','pairwise','type','spearman');
            end

            neg_log_corr_sp(:,i) = -log10(pCorr) .* sign(corr_sp);
        end

    end


    % if we are running in demo mode, calculate a t-SNE embedding for
    % visualization purposes and plot the output
    if nargin==0
        fprintf('%s: Plotting DEMO results\n',mfilename)
        % for visualization, let's calculate a t-SNE embedding
        matTSNE = tsne(matCoordinates);
        figure;
        subplot(1,2,1)
        scatter(matTSNE(:,1),matTSNE(:,2),15,matFeature,'filled');
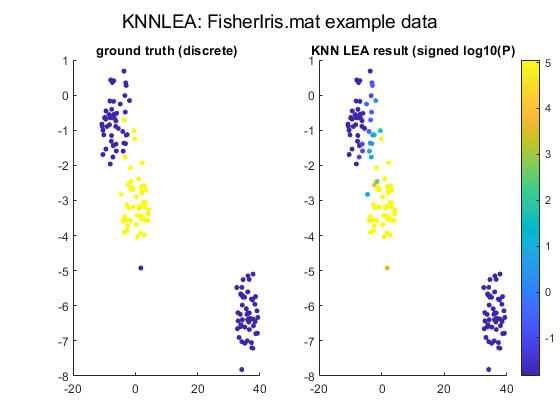
        title('ground truth (discrete)')
        subplot(1,2,2)
        scatter(matTSNE(:,1),matTSNE(:,2),15,matLEA,'filled');
        title('KNN LEA result (signed log10(P)')
        colorbar()
        suptitle('KNNLEA: FisherIris.mat example data')
    end

end % end of function

%%%%%%%%%%%%%%%%%%%%%%%%
% required subfunction %
function [a_counts,C]=countUnique(vec,matchgrouping)

    if nargin ==1
        [C,~,ic] = unique(vec);
        a_counts = accumarray(ic,1);
    else
        [Ctemp,~,ic] = unique(vec);
        temp = accumarray(ic,1);
        C = matchgrouping;
        a_counts = zeros(size(matchgrouping));
        a_counts(Ctemp)=temp;
    end

end


function x = fixinfs(x,infVal)
    % BS: set Infs to max and -Infs to min.

    if all(isinf(x)|isnan(x))
        warning('bs:BLA','%s: can''t fix infs or nans if all values are inf or nan',mfilename)
        return
    end

    if nargin<2
        x(isinf(x) & sign(x)>0) = max(x(~isinf(x)));
        x(isinf(x) & sign(x)<0) = min(x(~isinf(x)));
    else
        x(isinf(x) & sign(x)>0) = infVal;
        x(isinf(x) & sign(x)<0) = -infVal;
    end

end

knnlea: Running in DEMO mode
knnlea: Calculating local hypergeometric LEA scores
knnlea: Plotting DEMO results

ans =

   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    3.6517
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    2.6029
    5.0564
    5.0564
    5.0564
    5.0564
    1.7877
    5.0564
    1.7877
    5.0564
    1.1575
    5.0564
    5.0564
    5.0564
    5.0564
    1.1575
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
   -0.5361
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
    5.0564
   -1.8297
   -1.0172
   -1.8297
   -1.8297
   -1.8297
   -1.8297
    3.6517
   -1.8297
   -1.8297
   -1.8297
   -1.0172
   -1.8297
   -1.8297
   -1.0172
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
    0.3559
   -1.8297
   -0.5361
   -1.8297
    0.3559
   -1.8297
   -1.8297
    0.3559
    0.6862
   -1.8297
   -1.8297
   -1.8297
   -1.8297
   -1.8297
    0.6862
   -0.5361
   -1.8297
   -1.8297
   -1.8297
    1.1575
   -1.8297
   -1.8297
   -1.0172
   -1.0172
   -1.8297
   -1.8297
   -1.8297
   -0.5361
   -1.0172
   -1.8297
   -0.5361

Published with MATLAB® R2020b